Predicting the Unpredictable: Chaotic Dynamical Systems
Mathematics’ Meagan Carney Uses Probability and Dynamics to Predict
The only predictable part about life is that it is inherently unpredictable. Accidents happen. Conditions change. Life contains surprises.

Chaos Theory: Study of “Unpredictable” Outcomes
In mathematics, chaos theory is the study of apparently random or unpredictable outcomes. Chaos theory is often referred to as “the butterfly effect,” a term coined by mathematician Edward Lorenz, who used the example of a tornado being influenced by a minor event, such as a far-away butterfly flapping its wings several weeks earlier.
Meagan Carney, a Ph.D. student in mathematics at the University of Houston, has spent her time as a graduate student expanding on the mathematical principles and patterns underlying chaotic dynamical systems. Her research is advised by Matthew Nicol, professor of mathematics in the College of Natural Sciences and Mathematics.
Deterministic Systems: Initial Conditions Determine Outcome
In deterministic systems, the initial values determine the outcome. In deterministic chaos, unpredictability comes from the fact that two very similar initial conditions often lead to two very different outcomes.
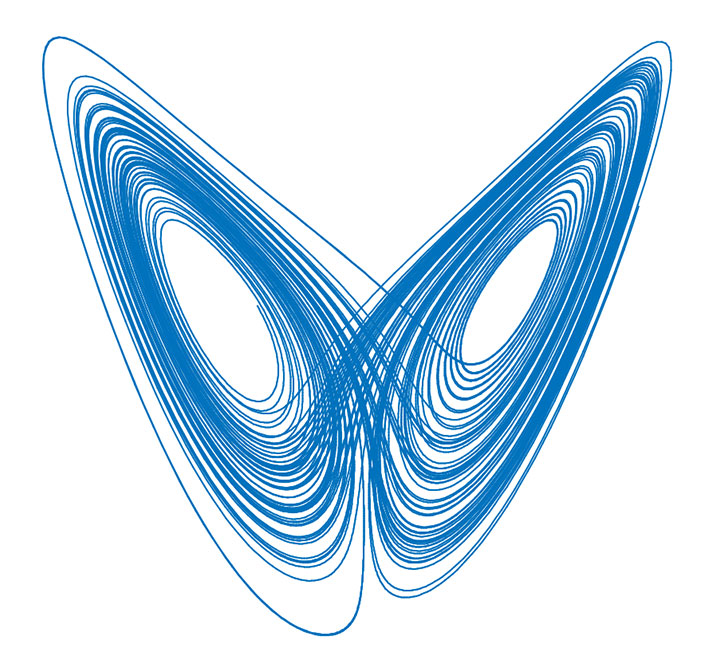
Although at face value, chaos appears to be completely random, there are underlying patterns.
“There is a randomness within the system, which is where the use of statistics comes in,” Carney said. “Our research establishes statistical properties, such as Central Limit Theorems and the Strong Law of Large Numbers.”
Statistical Properties Enable Predictions
One example would be weather. Even though day-to-day conditions can’t be forecast with complete certainty, in general, winter brings colder weather, while summer brings hotter temperatures.
These statistical properties enable certain predictions about chaotic dynamical systems.
“Instead of looking at the statistical properties of the averages in a system, we can also look at the statistical properties of the extremes in a system,” Carney said.
Examples of extreme events could be the probability of a 100°F day in March, a severe flooding event, or a major drop in the stock market.
During the course of her graduate studies, Carney has published two papers, with a third paper in submission, and attended conferences in cities as diverse as Marseille, San Francisco, Vancouver and Vienna.
“Meagan is a talented researcher who is not only adept at pure mathematics but also has a comprehensive science background and excellent computational skills,” Nicol said. “This is a rare combination of abilities.”
- Rachel Fairbank, College of Natural Sciences and Mathematics
January 16, 2019