Home Research Publications Teaching CV Collaborators



Geographic Variation in Body Size and Bergmann’s Rule
Body size of animals often increases with increasing latitude, a pattern known as Bergmann’s rule. Despite over a century of work on this classic biological rule, we still have a very poor understanding of the sources of selection that create one of the most broad-scale patterns known to biology. In general, latitudinal gradients in temperature are thought to be the underlying cause of Bergmann’s rule. The original explanation for Bergmann clines, as proposed by Carl Bergmann, was that a reduction in the surface-to-volume ratio of large animals vs. small animals allows large animals to survive colder temperatures at higher latitudes due to increased retention of metabolic heat. Yet, Bergmann clines also exist in many ectothermic animals which acclimate to ambient temperature very quickly. In addition, many other ecological and environmental variables change with latitude; for example, environments become systematically more seasonal with increasing latitude. However, few studies have explored the impact of these other ecological and environmental variables on selection, and thus their potential to generate Bergmann clines.
During my graduate work in the lab of Dr. Charles Fox, I showed that, at least in ectotherms, latitudinal gradients in temperature may not be responsible for generating Bergmann clines (my series of studies on this topic using the seed beetle, Stator limbatus, represents the only known example where an organism exhibits a Bergmann cline that is not due to a gradient in temperature). In a field survey, I examined how body size of S. limbatus varies geographically over a 38o range in latitude (Stillwell et al. 2007, American Naturalist) (Fig. 1). I found that body size increases with increasing latitude, following Bergmann’s rule (Fig. 2). I examined a total of 14 variables (13 environmental variables and 1 ecological variable) to see what variables could explain the latitudinal variation in size. I found that the variables that best explained the variation in size were: host plant seed size, seasonality and moisture availability. Mean temperature did not best explain the variation in size. In a follow up study, using artificially selected lines of beetles (large, control and small lines), I directly tested the hypothesis that the relative advantage of being larger (because being larger generally increases fitness) is greatest at cooler temperatures (Stillwell et al. 2008, Evolution). I found that the relative advantage of being larger did not change with temperature or was greatest at high temperature (the result varied among replicates), opposite to the prediction that selection favoring large size should be greatest at cooler temperatures. This, along with a few studies by other researchers, casts doubt on the hypothesis that latitudinal gradients in average temperature generate Bergmann clines, at least in this seed beetle.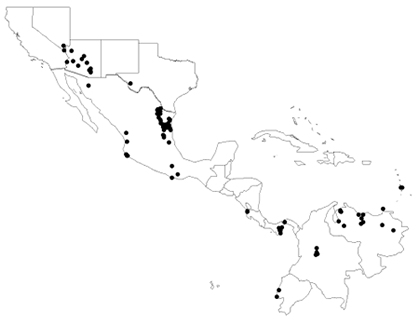

Figure 1. Distribution of collection localities of populations of Stator limbatus Figure 2. Males (top) and females (bottom) of Stator limbatus from Arizona, USA (left) and Colombia, South America (right). (photograph by Angela R. Amarillo-Suárez and Carlos E. Sarmiento) |
The Evolution of Sexual Size Dimorphism
A Developmental Perspective on Size Dimorphism
Males and females of nearly all animals differ in size, a phenomenon known as Sexual Size Dimorphism (SSD). The direction and magnitude of SSD varies considerably across taxa. For example, males are often larger than females in mammals, whereas females are often larger than males in insects. Most of this variation in SSD is due to three major sources of selection: (i) fecundity selection favoring large females, (ii) sexual selection favoring large males and (iii) selection for a shorter duration of growth and/or a faster growth rate and hence small size in both sexes (Stillwell et al. 2010, Ann. Rev. Entomol.). However, despite decades of research on evolutionary explanations for how selection can generate SSD, a major paradox remains unresolved: How do males and females evolve to be different sizes when they share the same genes that regulate growth and development? The variation in SSD we observe among organisms shows that this constraint can be overcome, but a sufficient explanation is still lacking.
Evolutionary quantitative genetic studies often measure the extent to which a shared genome between sexes can hinder the evolution of SSD. These empirical studies generally demonstrate that the genetic correlation (which measures a shared genome) for body size between the sexes is near 1.0 and that the heritabilities (which measure genetic variation and the ability to respond to selection) are similar between sexes. Therefore, we should expect little to no SSD in organisms, even with substantial selection differences between sexes. One caveat of nearly all prior studies is that they focused almost exclusively on the genetic architecture of adult body size in predicting the evolution of SSD. However, understanding how SSD evolves requires understanding how SSD forms during growth and development because the proximate target of selection is the sex-specific developmental process that produces adult SSD.
During my postdoctoral work in the lab of Dr. Goggy Davidowitz at the University of Arizona, I discovered that the key to answering this mystery lies in the developmental stages where male and female growth diverges. Using the hawkmoth, Manduca sexta, as a model system, I explored the genetic architecture of three physiological variables (see Stillwell and Davidowitz 2010 for a description of these variables) known to regulate body size in this insect during the last stage of larval growth. I found that females had considerably more genetic variation in the physiological mechanism that controls size (Stillwell and Davidowitz 2010, Proc. R. Soc. B; this study was cited or linked to in over 10,000 science web sites and blogs when it was published online ahead of print). As a result, females can respond faster to selection on body size than males, producing the female-biased (females larger) SSD found in M. sexta.
This work is novel because it reveals that studying how SSD forms during growth and development sheds new insights into how males and females evolve different sizes. This also opens up an exciting opportunity to study how internal factors (genetics, development and physiology) contribute to how SSD forms in animals, a very poorly understood area of SSD research.
Environmental Effects on Variation in Sexual Size Dimorphism
Although it is widely recognized that the magnitude of SSD varies among taxa, recent studies have shown that the degree of SSD, and sometimes the direction, also varies among populations within species. Much of this variation is genetically based and likely due to variation in the sources of selection that create SSD (see above section), primarily sexual selection, among species/populations. Alternatively, the effects of climate or other ecological and environmental variables may have different effects on males versus females, either because the fitness consequences of large versus small body size differs between the sexes or because the sexes differ in the degree of plasticity they exhibit in response to climatic or ecological variables. Many studies have examined how environmental factors affect phenotypic plasticity in body size, but few have examined how environmental factors affect SSD and the traits that mediate selection on male versus female body size.
During my graduate work, I showed that within-species variation in SSD can be generated by a gender difference in phenotypic plasticity in body size. Using the seed-feeding beetle, Callosobruchus maculatus, as a model system, I examined whether body size of males and females responded differently to variety of rearing temperatures. I found that although females were always larger than males, the degree of this SSD was greatest at intermediate temperatures (Fig. 3) (Stillwell and Fox 2007, Oecologia). My recent review paper shows that gender differences in body size plasticity are common in insects and likely play an important role in generating intra-specific variation in the degree of SSD (Stillwell et al. 2010, Ann. Rev. Entomol.).
During my postdoctoral work at the University of Arizona, I explored the proximate mechanisms that potentially create sex-specific plasticity in insects, using M. sexta as a model system. I found that larval size of males and females did not exhibit sex-specific plasticity when reared on different diet qualities or at different temperatures (Stillwell and Davidowitz in press, Proc. R. Soc. B). However, the sexes did exhibit sex-specific plasticity in the mechanism that controls size (i.e., the growth rate, the critical weight and the ICG); males and females exhibited sex-specific plasticity in the growth rate and the critical weight in response to both diet and temperature, whereas the ICG only exhibited sex-specific plasticity in response to diet. This study shows that sex differences in plasticity of physiological variables that control body size in M. sexta do not translate into sex differences in larval size because a change in one of these variables is counteracted by a change in one or more of the other physiological variables. These results reveal the complex way in which males and females respond to environmental variation differently and the consequences this has for SSD.
Studying sex differences in body size plasticity and the underlying mechanisms that produced these differences presents an exciting opportunity to understand how ecology and development interact to produce complex phenotypes.
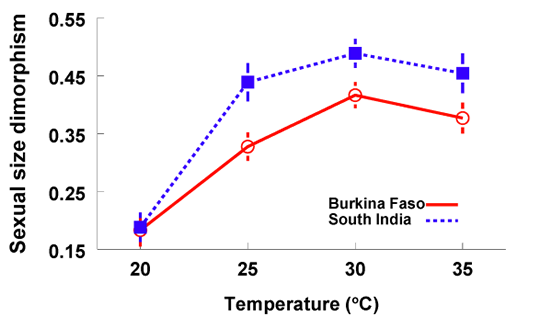

| Figure 3. The effect of rearing temperature on sexual size dimorphism of C. maculatus measured using the sexual dimorphism index (SDI) of Lovich and Gibbons (1992) |
Developmental Regulation of Morphological Scaling
The scaling of body parts of organisms with their overall size, a phenomenon called allometry, is a central feature of animal morphology that has intrigued biologists for over a century. Scaling of body parts ensures that all individuals of a population have a similar overall body shape despite considerable variation in size and that organs retain their form and function. The slope and intercept of these scaling relationships vary considerably among species, creating much of the variation in morphological diversity in animals. However, the proximate mechanisms that regulate scaling are poorly understood, offering a profound opportunity to examine how development shapes the evolution of complex phenotypes.
In my current postdoctoral position, I am working with Dr. Tony Frankino (University of Houston), Dr. Alex Shingleton (Michigan State University) and Dr. Ian Dworkin (Michigan State University) to examine the proximate mechanisms (physiological and genetic) that regulate morphological scaling, using the fruit fly, Drosophila melanogaster, as a model system. The proximate mechanisms that control scaling in D. melanogaster are a property of the physiological processes that determine final body size and organ size. As in M. sexta, there are three physiological variables that control the final body and organ size of D. melanogaster (see discussion of Stillwell and Davidowitz 2010, Proc. R. Soc. B for a detailed description of these variables). Consequently, different scaling relationships can only evolve through changes in one or more of these physiological variables.
To investigate how scaling relationship diversity evolves, I am using artificial selection to create novel wing size-body size scaling relationships in D. melanogaster (Fig. 4). At the end of selection (~ 12 generations), I will examine which of the physiological variables evolved in response to selection to determine how physiological processes create variation in scaling relationships. Furthermore, I will use the vast knowledge on the developmental genetics and physiology of D. melanogaster to dissect the genetic architecture (i.e., using array-based mapping methods to identify the genes involved in the regulation and evolution of scaling) of the response to selection.
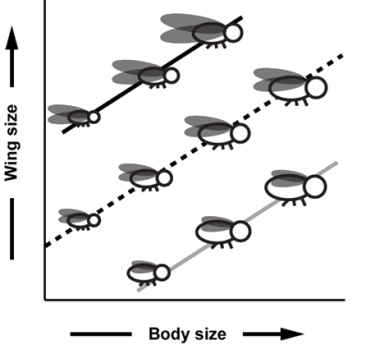
Figure 4. Lines depicting different scaling relationships in the fruit fly, Drosophila melanogaster. I am using artificial selection to generate lineages with different wing size-body size scaling relationships (small bodies with large wings vs. large bodies with small wings). Illustration by Max Westby. Right side: A silhouette of a fly wing. The pixel counts of wing silhouettes are used to measure wing size. A similar technique is used to measure pupal size (i.e., body size). |
Phenotypic Plasticity in Growth and Life History Traits
Phenotypic plasticity (a change in an organism’s phenotype in response to the environment) is a ubiquitous characteristic of nearly all organisms. Many types of environmental variables, such as temperature and diet quality, can induce plasticity, particularly during growth and development. Nearly all studies that have examined plasticity have examined the impact of a single environmental variable throughout development. However, organisms often grow and develop in complex environments where they are simultaneously exposed to variation in several environmental variables. In addition, environmental conditions experienced in different life stages can interact to produce complexity in plasticity (i.e., reaction norm shape at one developmental stage or along one environmental axis is affected by other developmental stages or other environmental axes). Yet, very few studies have explored how environmental conditions experienced in different life stages, or different environmental variables experienced in the same life stage, interact to produce complexity in reaction norm shape.
In previous work, I demonstrated that interactions between temperatures experienced early in life (immature stage) and later in life (adult stage) produce complex reaction norms for several traits in the seed beetle, Stator limbatus (Stillwell and Fox 2005, Ecology). In a separate study using the seed beetle, Callosobruchus maculatus, I showed that two environmental variables, host quality and temperature, interact in the juvenile stage to produce complexity in reaction norm shape in adults (Stillwell et al. 2007, Oecologia). In future work, I will continue to explore how plasticity evolves in complex environments by investigating interactions between multiple environmental variables at different life stages. I will also examine the physiology underlying complex patterns of plasticity in growth and life history traits. In addition, I will examine how genetic architecture of plasticity changes in complex environments to more accurately predict how plasticity evolves in nature, where environmental complexity is the norm.
