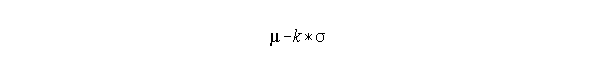
Quiz #1

Question 2.18

A set of data has a mean of 75 and a standard deviation of 5. You know nothing else about the size of the data set or the shape of the distribution.

1. What can you say about the proportion of measurements that fall between 65 and 85?
2. What can you say about the proportion of measurements that are less than 65?
   
   
   
   

Answers

1) Answer is based on Tchebysheff's Theorem. Lower bound formula (for a population data set) is

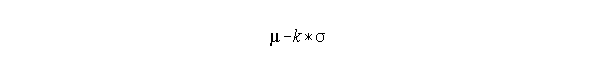
Upper bound formula is

The value for mu is 75, sigma is 5. First, one needs to find the value of k. Here the solution based on the lower bound formula.

65 = 75 - k*5

-10 = -k*5

-2=-k

k = 2.

If you used the upper bound formula, you would obtain the same value for k.

From lecture, you found

When k =2, p=0.75 or 75% of the proportion.

2) From question 1), you know that 75% of the values around the mean lie between 65 and 85. This means that 25% of the values are outside this region. The proportion of the region left than 65 is one half of 25% or 12.5%.