Understanding chemical reactions requires that we know something about how materials behave as the temperature and pressure change. For a single component (like quartz or ice) a unary phase diagram can be constructed by determining which phases are stable over a range of temperatures and pressures.
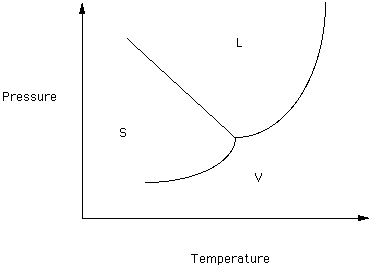
Figure 1
Note that three phases of this component exist over the depicted range of Temperature and Pressure - Solid, Liquid and Vapor. In the region labeled S, the solid form is thermodynamically stable. The curve separating the regions in which S and L are stable is the melting/crystallization boundary curve: melting if T is increasing and crystallization if T is decreasing. Similarly, the curve separating the Liquid and Vapor fields is the boiling/condensation curve. The curve separating the Solid and Vapor fields is the sublimation curve. If the T and P of the system is on the S-L boundary curve then solid and liquid are in equilibrium, Therefore, melting can take place over a range of T and P, For this system the melting temperature decreases as pressure increasers.
If the system solid-liquid is at equilibrium and the pressure is increased the phase with the highest density should be favored (that is, it should be thermodynamically stable).
Which phase, Solid or Liquid, has the highest density in this system?
The boiling-condensation and sublimation curves can be analyzed in a similar fashion.
We will be interested in the conditions of melting within the Earth. Note that in this system the slope of the melting curve is negative. If the slope were positive then an increase in P would cause:
If this boundary curve were vertical then an increase in P would cause
Two phases separated by a vertical boundary have identical densities.
Look at the boiling-condensation boundary curve. At low P which phase has the greatest density?
What is happening to the difference between the density of the liquid and the density of the vapor as pressure increases?
The critical point is the T and P at which the densities of the vapor and liquid forms of a component are identical. At higher temperatures and pressures there is no meaningful distinction between the liquid and vapor phases. Some authors refer to material above its critical point as a supercritical fluid.
The question ..."what is the melting point of X" can only be answered by asking ..."at what pressure". To give a unique melting point requires that the pressure be fixed. By convention we refer to the standard melting point of X as the temperature at which liquid X and solid X are in equilibrium at 1 atmosphere (14.7 pounds/square inch) to total pressure. In Figure 2 the 1 atm line (an isobar or line of equal pressure) has been drawn to represent the reference pressure. The intersection of this isobar with the melting curve defines the standard melting temperature (Tm)
What happens to the boiling temperature if the pressure is less than one atmosphere? Near the top of Mt. Everest the temperature of boiling water would be________
than the temperature of boiling water in Houston, Texas.
If you heat water at one atmosphere pressure at 100oC it will boil. The temperature of water can not exceed this value. What might you do to be able to heat water to a temperature above 100oC.?
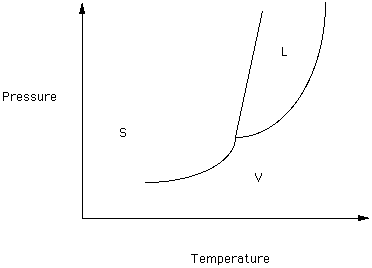
Figure 2
Look at the unary phase relationships in Figure 2.
Which phase (S or L or V) has the greatest density?
Most solids behave like Figure 2. Figure 1 represents the behavior of a few substances (like water) where the density of the solid is less than the density of the liquid.
Kyanite (K), Sillmanite (S), and Andalusite (A) are three polymorphs of Al2SiO5 (Figure 3).
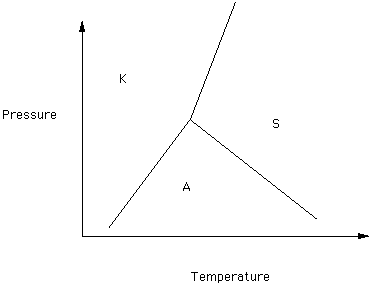
Figure 3
Click on the phase which has the greatest density for each of the following pairs:
The triple point is the T and P at which all three phases are in equilibrium. Just for grins, we will see what theory says the temperature and pressure are at the tripple point. Two forms will appear. On the first check off kyanite, sillmanite, and andalusite. Click on submit. On the second form do not check any of the options and click on submit. Look at the magnitude of the error ellipse.
Thermodynamics
In addition to the total pressure acting on a system it will be necessary to consider the effect of the partial pressure of different components on solids. A hydrous solid is one that contains H2O or (OH) and an anhydrous solid contains neither. Similarly, some solids contain CO2 (calcite - CaCO3) whereas other do not (quartz - SiO2).
Consider the effect of the partial pressure of H2O on quartz - SiO2) as depicted in Figure 4.
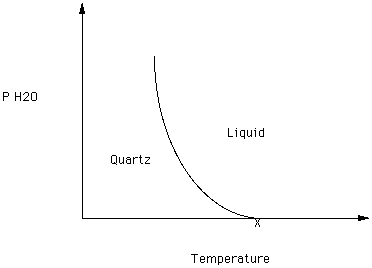
Figure 4.
Quartz melts at XoC at a partial pressure of H2O of zero. What happens to the melting point of quartz as the partial pressure of water increases?
Recall that some phases contain water or hydroxyl - micas and amphiboles, for example. The effect of increasing the partial pressure of water on the melting point of a mica is illustrated in Figure 5
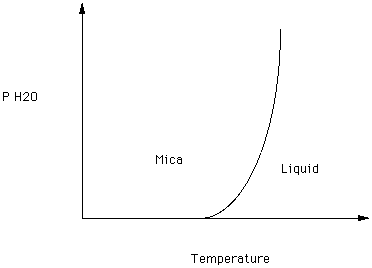
Figure 5.
What happens to the melting point of mica as the partial pressure of water increases?
The melting curves for mica and quartz are superimposed in figure 6.
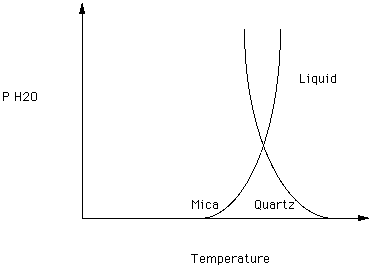
Figure 6.
Note that at low partial pressures of water quartz melts at a higher temperature than mica melts. Above the pressure defined by the intersection of the two curves, quartz melts at a lower partial pressure of water than does mica. Thus, variations in the partial pressure of water could cause variations in the sequence of crystallization of two or more phases.
In general, if a solid contains a "volatile" (like water, OH-, F- or Cl-) then an increase in the partial pressure of that volatile will result in an increase in the melting temperature of the solid.
Given this generalization,what kind of melting behavior expected for calcite in the presence of carbon dioxide? (Hand in your sketch of the diagram)

Figure 7
What kind of melting behavior is expected for quartz in the presence of carbon dioxide?
Binary Phase Diagrams
Unary phase diagrams will not let us get very far towards being able to understanding melting and crystallization because most rocks contain two or more minerals (phases). Consider two unary phase diagrams, one for phase A and one for phase B. If we were interested in the behavior of all possible mixtures between pure a and pure B then we would need three dimensions - Temperature, Pressure, and Composition (see Figure 8.
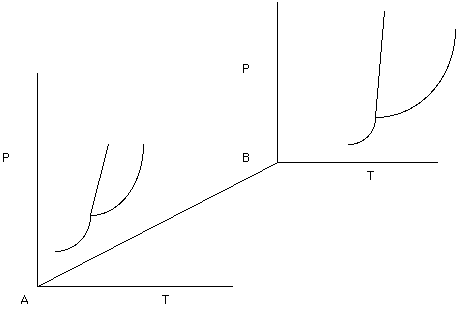
Figure 8.
This would make representation a little more difficult. To reduce the number of variables needed for representation, we could agree to work at constant pressure. In Figure 9. the 1 atm isobar has been added. We will work with the plane Composition-Temperature but remember that we could have worked with any constant pressure slice.
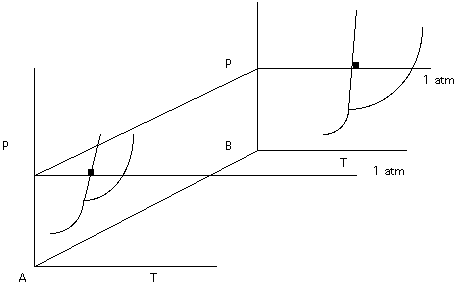
Figure 9.
The melting points of A and B in Figure 10 are marked with a square.
(the intersection of the solid-liquid boundary curves with the 1 atm isobar). For ease in representation the plane in Figure 10 will be reoriented and * will be used to represent the melting temperatures of A and B.

Figure 10
Above the melting point of Solid A is a liquid (L) of composition A. Similarly, for phase B. The composition axis connects the compositions A and B. Each point along this axis has two values - the amounts of A and B. For example, A represents 100% A and 0% B. A point half way between A and B would be 50% A and 50% B. The composition axis is reproduced in Figure 11. This construction is termed the lever rule.

Figure 11.
Composition C lies in between A and B and closer to A. The line segment AB represents 100% of the system. To determine the amount of B in composition C we would start at 0% B and count over until we reached C. That is, the ratio of line segment AC to line segment AB is proportional to the amount of B in composition C; about 33%. The ratio of line segment CB to AB gives is proportional to the amount of A in composition C; about 67%. Given any line segment which connects the compositions of two phases, you can graphically determine how much of each phase is present in some intermediate composition.
Consider a sample of 100% A which is at its melting point - solid and liquid coexist at equilibrium. A small quantity of B is added to the system. B could enter the high temperature form of A (liquid) to a greater extent than the low temperature form of A (the solid). In this case the transition form the low to high temperature form of A will be lowered; that is, B would cause the melting temperature of pure A to be lowered.
If B enters the low temperature form of A to a greater extent than it enters the high temperature form of A the transition from low to high is increased. That is, the melting temperature of A would be increased by the presence of B.
If B preferentially enters neither the high or low temperature form of A the transformation temperature is unchanged.
No Intermediate Compounds, No Solid Solution and A Single Liquid
In this class of diagrams there are no compounds of intermediate composition formed, the end members of the system do not enter into a solid solution relationship and only a single liquid is formed upon melting. Each end member has the effect of lowering the melting temperature of the other.
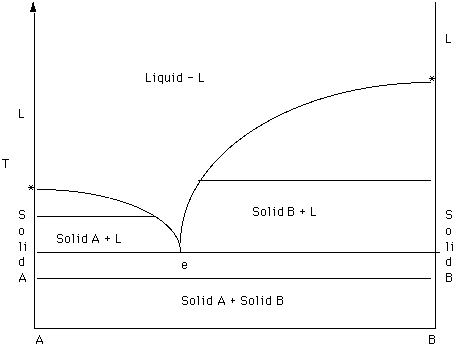
Figure 12
Recall that the * mark the melting temperatures and A and B. Note the two curves that descend towards the middle of the diagram from the melting points. These are the two liquidus curves. A liquidus curve separates a field of a single liquid from a field in which a solid and a liquid coexist in equilibrium.
The first step in analyzing a phase diagram is to label the fields. The first rule is to draw a line across each field - a two-phase tie line or a Schrinemacher line. Look at the ends of each line; the compositions of the end of the line indicate what phases are stable in each field.
For example, look at the field above the liquidus curves. One end intersects liquid A and the other liquid B. Since there is only one liquid (see the heading given above) a single liquid exists in this field. To determine the composition of any point in this field drop a perpendicular line to the composition reference axis and use the lever rule to determine the bulk composition of the liquid.
In the field labeled Solid A and liquid, a two phase tie line intersects the Solid A side of the diagram and the liquidus. Note that each two phase tie line always intersects pure A but a liquid with a different bulk composition. The field of Solid B + liquid behaves in a similar fashion. The 4th field is labeled Solid A plus Solid B.
The next step in interpretation is to follow the behavior of some bulk composition during cooling or heating or both. In this way you begin to become familiar with what is happening during crystallization and/or melting.
In Figure 13 the composition of interest is Z.
- The first step is to determine the bulk composition by using the lever rule on the composition axis. In this case the bulk composition is about 80% A and 20% B. We will assume that the bulk composition does not change during our analysis.
- The second step is to draw a line perpendicular to the
composition axis through the bulk composition of interest. This composition vertical will serve as a reference line.
- The third step is to look at the fields intersected by the composition vertical. In this case the reference line goes from a field on a single liquid through a field where solid A and a liquid of variable composition coexist and finally into a field where solid A and solid B coexist.
- The fourth step is do do a more detailed analysis. Pay particular attention to where the composition vertical crosses any field boundaries and use the lever rule when appropriate.

Figure 13.
The temperature at which the composition vertical intersects the liquidus curve marks the temperature at which solid A becomes saturated in the liquid. Crystals of A should nucleate at the temperature. If nucleation is prevented the liquid would continue to cool and A would become supersaturated in the liquid. When A begins to precipitate from the liquid, the liquid is enriched in B. Recall that the bulk composition remains unchanged throughout the analysis.
The liquid changes composition along the liquidus curve; thus the liquidus marks the path of evolution of the liquid during cooling. A remains constant in composition throughout; note that the left hand side of the field is bounded by the composition of pure A. At the intermediate temperature given by the two phase tie line A and liquid coexist in amounts of about 60% L and 40% A. (Confirm this by applying the lever rule) The composition of the liquid is given by dropping down to the composition axis - about 67% A and 33% B.
The two liquidus curves intersect in a point - the eutectic. The horizontal line through the eutectic connects the composition of 3 phases that coexist at equilibrium - A, B, and a liquid of eutectic composition. The Gibs Phase Rule defines the following relationship between the number of phases, components and degrees of freedom (in our case pressure was fixed (1 atmosphere) so the expression is:
p + DF = c +1
C equals 2 (a binary) so
p + DF = 3.
At the eutectic there are 3 phases so there are zero degrees of freedom. To get a feeling for degrees of freedom consider the situation in which the temperature of Z is above the liquidus:
1 + DF = 3
or DF = 2.
A single liquid is present and to describe the system to someone you would need to give the temperature and the composition of the liquid; the intersection of the temperature and composition lines define a unique point. When solid A and a liquid are present,
2 + DF = 3
or DF = 1.
If you tell someone that the system contains solid A and a liquid you can uniquely define the system by giving either the composition of the liquid or the temperature.
Thus, the number of degrees of freedom is the least number of variables (such as T, P, and composition) needed to uniquely define the system. In other sources you will see the phase rule given as
p + DF = c +2
Remember that in our binary systems the pressure was fixed at a constant value of 1 atmosphere so the 2 is reduced to a 1. Therefore, at the eutectic horizontal the level rule can not be applied. You should use the lever rule immediately above and immediately below the eutectic horizontal and "deduce" what reactions are taking place. Above the eutectic the system consists of about 50% A and 50% liquid of composition e. Below, the system consists of 80% A and 20% B. Therefore, at the eutectic temperature, the liquid is all used up in the precipitation of 30% A and 20% B. If you were cooling Z and recording the variation in temperature as a function of time you would find that the temperature would reach the eutectic and remain constant for however long it took for the reaction to take place. Remember that phase diagrams are based on thermodynamics and do not contain information about the time it takes to reach equilibrium or how equilibrium is reached.
Draw the composition vertical X corresponding to 75% B and 25% A. Cool this composition and describe what happens. (Hand in this diagram
The first solid phase to appear on cooling is:
Heating is the reverse of cooling. Heat composition Z. Note that the mixture remains all solid until the eutectic is reached. The temperature remains constant until about 50% of the sample melts leaving solid A and a liquid.
The intervals of A plus liquid and B plus liquid can be termed the intervals of partial melting or partial crystallization. Usually we think about a solid having a unique melting point; however, in the case of a mixture of A and B, there is only one composition which totally melts at one temperature. What is that composition?
Materials can exhibit different responses when they are heated:
- congruent melting - Solid A goes to a liquid of the same composition
- incongruent melting - solid A goes Solid B plus liquid C
- decomposition - a solid breaks down without the production
of a liquid.
Systems With A Compound Of Intermediate Composition
Zircon (ZrSiO4) is a minor constituent in many granitic rocks. The following phase diagram shows what happens when Zircon is heated.
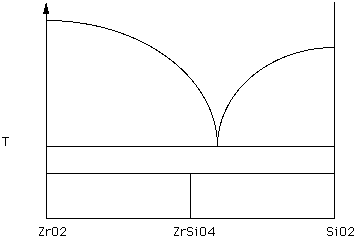
Figure 14.
Label the diagram using the procedures outlined in the previous section. Starting with Zircon, describe what happens as this material is heated. (Hand in this diagram)
Note that there are two 3-phase tie lines in the diagram. One connects ZrO2, a eutectic liquid, and SiO2. The other connects ZrO2, ZrSiO4, and SiO2.
In Figure 165a phase diagram with an intermediate composition (AB) forms. AB melts congruently (goes to a liquid of composition AB). If you follow the composition AB it goes directly to a liquid at its melting temperature. Note that this diagram looks like two of the simple binary phase diagrams. The composition AB remains a solid until the temperature corresponding to the "hump" is reached. Note that this hump is a thermal divide. Compositions to the right move toward B and compositions to the left move toward A.
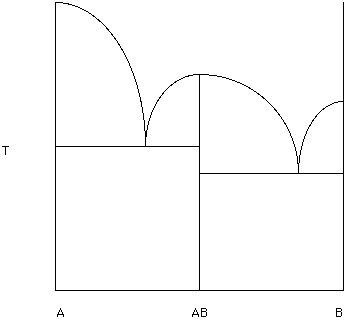
Figure 15.
Label each field (Hand in this diagram). Select a bulk composition equal to 50% AB and 50% A. What is the first solid to appear when a liquid of this composition is cooled to the liquidus?
Locate the bulk composition equal to 80% B and 20% AB. Which solid remains just above the eutectic temperature?
Compounds that melt incongruently have played a major role in our thinking about igneous rocks. Bowen noted that at 1 atmosphere total pressure, enstatite melted to form olivine plus a liquid. During cooling, olivine reacted with a liquid to form enstatite. This experimentally determined result lead Bowen to propose the discontinuous side of the reaction series. Incongruent crystallization is the discontinuous reaction that is referred to. Recall that the other side of the reaction is termed the continuous side of the reaction series as there is a complete solid solution between albite and anorthite (plagioclase). A schematic of Bowen's Reaction series is given in Figure 16.
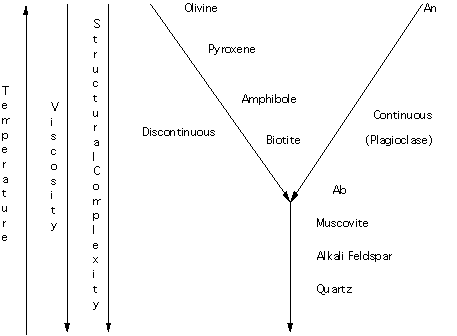
Figure 16.
Temperature is increasing upwards. Viscosity (a measure of the resistance to flow of a liquid) decreases downwards. Silicates at the high temperature end have simple structures (isolated tetrahedral for olivine and single chain for pyroxene) whereas those at lower temperatures have more complicated structures (framework for feldspars and quartz).
The role of water is critical. In the reaction series it is assumed that water is present so that amphibole and micas can form. In the absence of water these phases can not crystallize. As will be noted elsewhere water can lower the viscosity of the melt.

Figure 17.
Label the fields in the diagram in Figure 17 (Hand in this diagram). Note that if you follow the composition of Enstatite (the solid line) it terminates in the field of olivine plus liquid (hence the incongruent melting behavior of Enstatite). In other words, if you heated enstatite it would form an olivine plus a liquid. [This is only true at relatively low pressures - < 10Kb]
The point p is the peritectic. Note that a three phase tie line runs through p and connects the compositions of olivine, enstatite and liquid off composition p. If a liquid of composition Enstatite is cooled olivine is the first phase to crystallize. As temperature drops olivine continues to precipitate and the liquid changes composition along the liquidus. At the peritectic horizontal three phases are in equilibrium. Below the peritectic horizontal only Enstatite remains. Therefore, at the peritectic, Olivine reactions with liquid p and crystallizes Enstatite.
Select a composition of half olivine and half pyroxene. Draw in the composition vertical and follow the crystallization behavior. Note that olivine is "over produced" just above the peritectic horizontal; that is, there is more olivine above the peritectic than there is below. In Bowen's words, "olivine reacts with a liquid to produce a pyroxene".
Select the composition that is about 80% enstatite and 20% quartz. What is the first mineral to appear on the cooling of that liquid?
How much olivine is present below the peritectic?
Therefore:
Start with a liquid that is 50% olivine and 50% enstatite. At equilibrium, the solid that forms will not contain which of the following minerals?
Imagine a situation in which olivine is removed from the liquid at the peritectic p. Perhaps it sinks because of its high density. When crystals are subtracted from a liquid (crystal fractionation) the remaining liquid is treated as a new liquid.
What solids will liquid p yield when crystallized?
Approximately how much enstatite and quartz can be produced in this manner? (remember that some of the olivine was removed at p)
Note that this diagram tells us that olivine (at least the Mg-rich variety) and quartz are incompatible. That is, they will not coexist at equilibrium. I have found that compatability relationships are very helpful in identifying minerals.
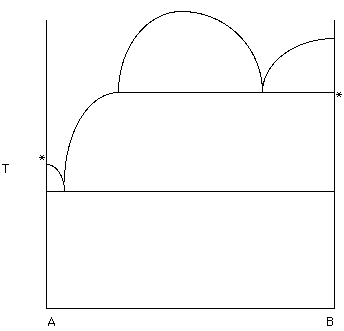
Figure 18.
The phase diagram in Figure 18 may look "strange". However, keep in mind that the melting temperatures of A and B are indicated with a *. Therefore, there is solid B below B* and liquid B above B*. Label the diagram. [Hint ... the "half-football shape" defines a region of liquid immiscibility - Hand in this diagram].
Solid Solutions
Recall the some systems exhibit solid solution. For example, Albite and Anorthite exhibit a "complete" range of substitution of [Na + Si] for [Ca + Al] in the plagioclase series. Size, charge, structural position (coordination number) and bond preference are variables which control the extent to which one ion can substitute for another. The plagioclase series is depicted in Figure 19. What effect does anorthite have on the melting temperature of albite? .
What effect does albite have on the melting temperature of anorthite?
There is a single liquidus curve which separates a region of one liquid from a region of liquid plus solid. In this case the solid is changing composition and the composition of the solid at any temperature is given by the solidus. Taken together the liquidus and the solidus form a lens within which liquid and solid solution coexist.
For the bulk composition 50% Ab (albite) and 50% An (anorthite) the composition vertical crosses a field of liquid, the liquid plus solid solution field and a field of solid solution. The upper most two phase tie line illustrates that the first formed solid solution is enriched in An and that the last liquid to disappear on cooling is enriched in Ab. At any temperature the two phase tie line connects the composition of the liquid in equilibrium with the solid solution. Drop a perpendicular from an end of the tie line to the composition reference axis to determine the exact composition. The lever rule can be used to determine the percentages of solid solution and liquid present at that temperature.
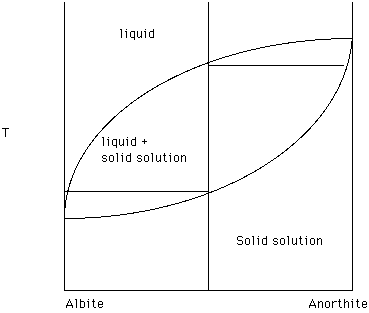
Figure 19.
The diagram tells us that a finite drop in temperature requires the solid solution phase to change composition in order to be in equilibrium with the liquid. This means that the solid solution phase must be homogeneous - the same chemical composition throughout the solid solution phase. As these crystals grow larger it takes longer for this homogenization to occur. Again, thermodynamics does not address rates of reactions. Many plagioclase crystals are chemically zoned with the center of the crystal richer in An and the margins richer in Ab. This reflects disequilibrium crystallization.
A solid solution series with a minimum is illustrated in Figure 20. Note that as crystallization occurs the remaining liquid moves toward the minimum.
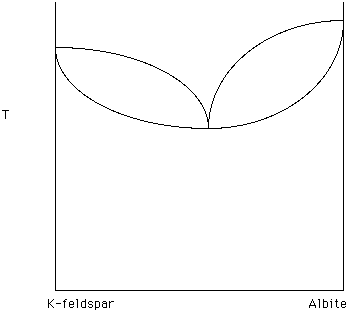
Figure 20.
The system k-feldspar and albite looks, at high temperatures, like the binary system in Figure 21. At low temperatures there is a complication below the solidus (see Figure 21). Note that this "hump" looks like the liquid immiscibility gap in Figure 18except that this is a region within which a homogeneous solid solution unmixes or exsolves into two solid solutions. This type of gap is termed a solvus.
The arrows next to the gap show the direction of change of composition. As the temperature decreases the two solid solution phases continue to separate from each other and approach, but do not reach, the compositions of the two end members. The level rule can be used within the exsolution gap to determine the percentages of the two phases present at that temperature.
Label the diagram (Hand in this diagram and cool composition X.

Figure 21.
When an alkali feldspar solid solution cools slowly the alkali feldspar will exsolve into a K-rich phase and an Na-rich phase. This texture is termed a perthite if K-rich > Na-rich or an antiperthite if Na-rich > K-rich. The top of the gap is at about 660oC at 1 atm pressure. If the alkali feldspar solid solution is cooled rapidly it may unmix but the unmixing would not be evident without magnification. This is termed a microperthite. If the phase is cooled so rapidly that it does not unmix but remains a single phase it is called anorthoclase. Anorthoclase is not stable in a thermodynamic sense at surface temperatures and is metastable.
Disequilibrium Crystallization
In Figure 22 a binary phase diagram is given in which there are three incongruent melting compounds of intermediate composition - C, D, and E.
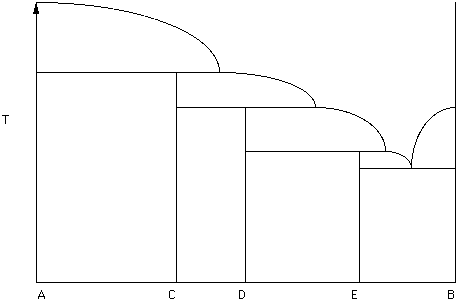
Figure 23.
Label the diagram (Hand in this diagram Select a composition consisting of 50% A and 50% C. Under equilibrium conditions is there any way that some other phase (C, D, E or B) could crystallize from this liquid?
Recall that at a peritectic, crystals must remain in contact with the peritectic liquid so that if the crystals are separated from liquid at Tp, the liquid must be considered to be a new liquid.
Bowen thought that silica-rich liquids (like granite) could be produced from mafic-rich liquids (basalts) by separation of crystals from liquids at peritectic points. Start with 100 grams of liquid of a composition half-way between A and B. Separate crystals from liquids at each peritectic point. How much of the silica-rich phase do you end up with?
Bowen did not know that the mica and amphibole phases must crystallized in the presence of water or some other volatile and he assumed that a peritectic relationship existed between amphibole and mica. In fact, the peritectic relationship between pyroxene and olivine is present only at relatively low pressures (less than about 10Kb). What depth is 10Kb equivalent to? At higher pressures, enstatite melts congruently. Sketch the high pressure phase diagram.

