Today let's ask: Can we hear shapes? The University of Houston Math Department presents this program about the machines that make our civilization run, and the peoplewhose ingenuity created them.
In 1966 the famous mathematician Mark Kac asked: "Can one hear the shape of a drum?" Kac was not really interested in synesthetesia — he was asking a deep mathematical question. This is what he meant: Anybody who has played a guitar will know that the note being sounded depends on the length of the vibrating string. If you press a string against the fifth fret, the plucked string will produce a higher note than when pressed against the third fret.
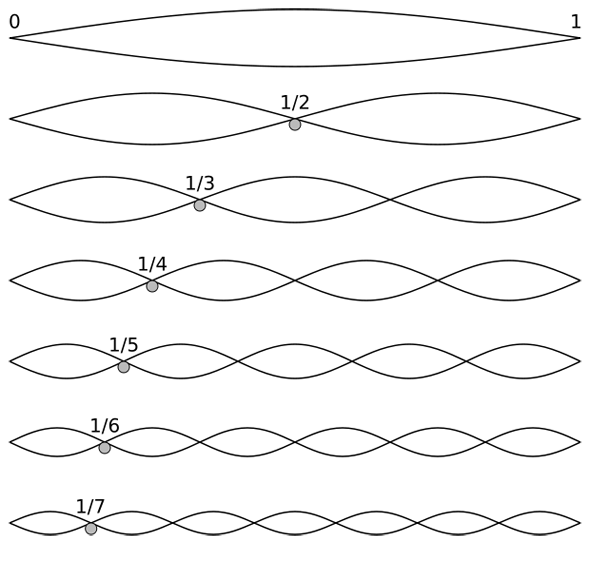
A sounded string produces a sound by vibrating at different frequencies. Shown are the first seven modes of vibrations which produce the seven lowest frequencies when an open string is sounded.
Now, lets turn this around: If you can determine the pitch of the sounded note, you can determine the fret that was depressed. You can hear the length of the string.
Unlike a guitar, a drum does not produce a sound with a definite pitch. It is not possible to play a melody on a drumset. There is a deep mathematical reason for this — the string of a guitar can be described by an equation in one spatial dimension. However, to describe the vibrations of a drumhead we need two spatial dimensions. Why does this difference in dimension matter?
When you sound an instrument you produce air vibrations at many different frequencies. The particular mix and intensity of these frequencies determines the quality of the produced sound: it let's you tell apart a guitar from a violin and a piano.
Now, instruments that cause vibrations in one dimension produce frequencies that are multiples of one another. A sounded drum, on the other hand, results in frequencies that are related in a far more complicated way. Indeed, the frequencies that are produced when you strike a drum are intimately related to the shape of the drum: a round drum will sound differently from a square or octagonal drum. This is true even if the drums are made of the same material, and their areas are the same. And, none of these drums will produce a sound with a definite pitch.


Left: Photo showing the complex pattern of the complex vibration of a string. Right: Like a string, a sounding a membrane (say, a drumhead) excites different modes of vibration, each of which oscillates at its own frequency. Shown is one such mode.
We can now make sense of the question that the mathematician Mark Kac asked: Can you tell the shape of a drum from its sound? Kac showed that you can determine the area and circumference of the drum from its sound. However, he did not know whether you can determine its shape, that is, whether each shape produces its own signature collection of frequencies. This question stayed unanswered for a quarter of a century, until in 1992 mathematicians gave an example of two differently shaped drums that sound exactly the same. The answer to Kac"s question is therefore "No, you cannot always hear the shape of a drum".
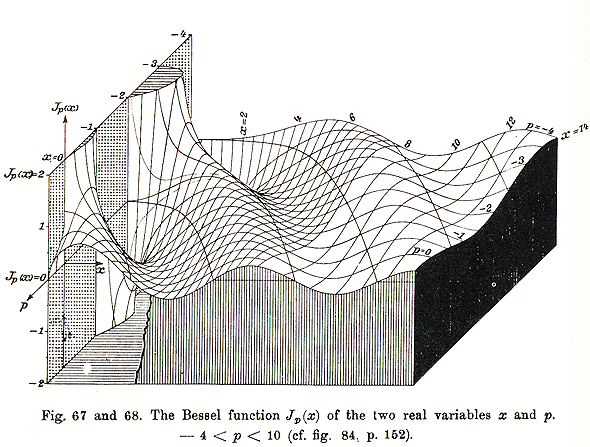
The frequencies produced by a round drumhead are given by the zeroes of a special type of function called the Bessel function. Source: E. Jahnke and F. Emde, Tables of Functions with Formulae and Curves. (New York: Dover Pubs. 1945. Originally published in 1933): pg. 126.
Some physicists think that all matter is comprised of very small oscillating strings, and that our universe is contained in a moving membrane. They propose that the frequencies of these vibrations determine the properties of all that is. If these string theorists are right, then our entire universe truly is a symphony produced by the sounding of countless tiny instruments.
I'm Kreso Josic, at the University of Houston, where we're interested in the way inventive minds work.
Excellent descriptions of percussion instrument can be found in T. Rossing"s book The Science of Sound, Addison-Wesley, 2001, and The Science of Percussion Instruments, World Scientific Publishing, 2000.
I highly recommend Bill Sethares" webpage and book Tuning, Timbre, Spectrum, Scale, Springer, 2nd edition, 2004. It"s a bit off the wall, but lots of fun to read. Bill Sethares" music is also eye (or rather ear-) opening http://eceserv0.ece.wisc.edu/~sethares/xentone.html.
Brian Green"s The Elegant Universe provides and excellent popular introduction to modern physical theories about the structure of the universe.
All images, other than the Bessel function graph, are courtesy of Wikipedia Commons.